
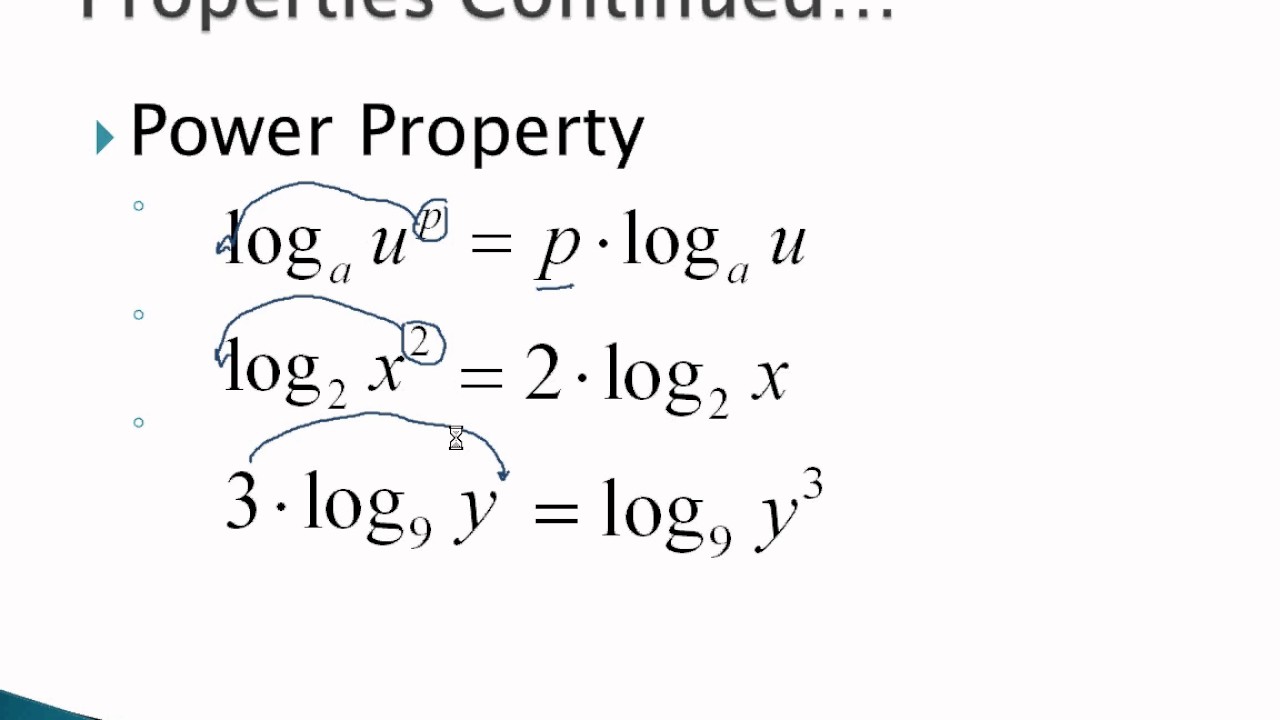
And we don't mean just any sum - we mean adding logs with multiples.
#Log condense calculator how to#
We'll now use it (together with the product property) to learn how to add logs.
Let's turn it around, fix the notation to suit the one used in the condense logarithms calculator, and have it neatly here for future use:
#Log condense calculator full#
Mind you, we'll keep to formulas for now, and once we have them in full glory, we'll move on to condensing logs examples in the last section.įirst of all, we take on the simplest of the expanding formulas: that for a logarithm of an exponent. We now take the theory on how to rewrite logarithms and work its magic to our needs. The three combined are what the condense logarithms calculator is all about. That way, we obtain formulas for adding logs, subtracting logs, and multiplying logs by a number. However, if we look at them backward, they write the expression as a single logarithm.

After all, whatever we raise to power 0, we get 1.

We denote them ln(x) and log(x) (the second one simply without the small 10), and their bases are, respectively, the Euler number e and (surprise, surprise!) the number 10. There are two very special cases of the logarithm which have unique notation: the natural logarithm and the logarithm with base 10.For example: ³√64 = 4īefore we learn how to rewrite logs, let's mention a few critical facts concerning them. However, as opposed to logarithms, roots return the exponent base, not the exponent itself (in the above language: they return how many people get infected by a single person). Note that taking a root is also considered an inverse operation to taking a power. In the above epidemic example, the logarithm (with base 4) returns at which step we get a fixed number of infected. Note, however, that in general, this can be (calc:1503). 💡 logₐ(b) gives you the power to which you'd need to raise a in order to obtain b. To make it all precise, let's see the following log definition. The logarithm is the inverse function to the exponential one. In general, we describe the number of sick in the n-th step by the exponent 4ⁿ. In turn, they got 4² = 4 * 4 = 16 people infected, who later got 4³ = 4 * 4 * 4 = 64 people infected. Indeed, if we assume that each infected person transmits the disease onto, say, 4 others, then patient zero got 4 people sick. Mathematically speaking, such a thing is called exponential growth.Īs you might have noticed, the name suggests that it has something to do with exponents. With the COVID-19 pandemic raging on, there's been quite some talk about the rate at which the number of cases increases over time.


 0 kommentar(er)
0 kommentar(er)
